LeetCode - Path Sum III

Problem statement

Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.

The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).

Problem statement taken from: https://leetcode.com/problems/path-sum-iii

Example 1:

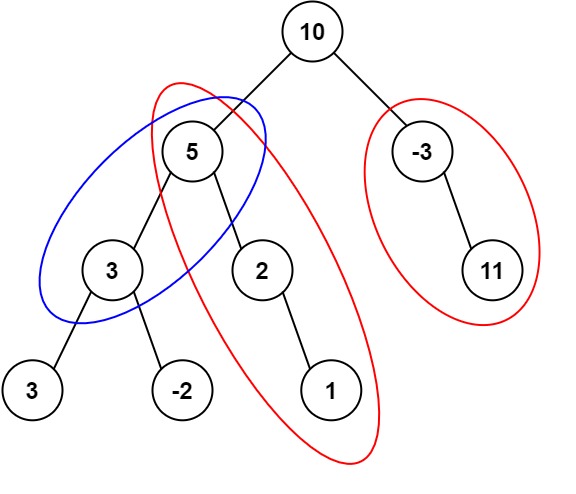
Container

Input: root = [10, 5, -3, 3, 2, null, 11, 3, -2, null, 1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.

Example 2:

Input: root = [5, 4, 8, 11, null, 13, 4, 7, 2, null, null, 5, 1], targetSum = 22
Output: 3

Constraints:

- The number of nodes in the tree is in the range [0, 1000].
- -10^9 <= Node.val <= 10^9
- -1000 <= targetSum <= 1000

Explanation

Recursion

The problem is similar to our previous blog posts Path Sum and Path Sum II.

We need to change the algorithm a bit to count the different paths in the tree. We will use the DFS algorithm to count the paths. Let's check the algorithm.

// pathSum method
- if root == null
  - return 0

- return dfs(root, 0, targetSum) +
    pathSum(root->left, targetSum) +
    pathSum(root->right, targetSum)

// dfs method
- if root == null
  - return 0

- set currentSum = previousSum + root->val
      count = 0

- if currentSum == targetSum
  - count = 1

- return count +
    dfs(root->left, currentSum, targetSum) +
    dfs(root->right, currentSum, targetSum)

The time-complexity can be reduced to O(nlog(n)) by reversing the linked list.

Let's check our algorithm in C++, Golang, and Javascript.

C++ solution

class Solution {
public:
    int dfs(TreeNode* root, long long previousSum, long long targetSum) {
        if(root == NULL) {
            return 0;
        }

        int currentSum = previousSum + root->val;
        int count = 0;

        if(currentSum == targetSum) {
            count = 1;
        }

        return count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum);
    }

    int pathSum(TreeNode* root, int targetSum) {
        if(root == NULL) {
            return 0;
        }

        return dfs(root, 0, targetSum) + pathSum(root->left, targetSum) + pathSum(root->right, targetSum);
    }
};

Golang solution

func dfs(root *TreeNode, previousSum, targetSum int) int {
    if root == nil {
        return 0
    }

    currentSum := previousSum + root.Val

    count := 0

    if currentSum == targetSum {
        count = 1
    }

    return count + dfs(root.Left, currentSum, targetSum) + dfs(root.Right, currentSum, targetSum)
}

func pathSum(root *TreeNode, targetSum int) int {
    if root == nil {
        return 0
    }

    return dfs(root, 0, targetSum) + pathSum(root.Left, targetSum) + pathSum(root.Right, targetSum)
}

Javascript solution

var dfs = function(root, previousSum, targetSum) {
    if(root == null) {
        return 0;
    }

    let currentSum = previousSum + root.val;
    let count = 0;

    if(currentSum == targetSum) {
        count = 1;
    }

    return count + dfs(root.left, currentSum, targetSum) + dfs(root.right, currentSum, targetSum);
};

var pathSum = function(root, targetSum) {
    if(root == null) {
        return 0;
    }

    return dfs(root, 0, targetSum) + pathSum(root.left, targetSum) + pathSum(root.right, targetSum);
};

Dry Run

Let's dry-run our algorithm to see how the solution works.

Input: root = [10, 5, -3, 3, 2, null, 11, 3, -2, null, 1]
       targetSum = 8

// pathSum method
Step 1: if root == NULL
          root -> 10
          false

Step 2: dfs(root, 0, targetSum) + pathSum(root->left, targetSum) + pathSum(root->right, targetSum)
        dfs(->10, 0, 8) + pathSum(->5, 8) + pathSum(-3, 8)

// dfs method
Step 3: if root == NULL
          root -> 10
          false

          currentSum = previousSum + root->val
                     = 0 + 10
                     = 10

          count = 0

          currentSum == targetSum
          10 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->5, 10, 8) + dfs(->(-3), 10, 8)

// dfs(->5, 10, 8)
Step 4: if root == NULL
          root -> 5
          false

          currentSum = previousSum + root->val
                     = 10 + 5
                     = 15

          count = 0

          currentSum == targetSum
          15 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->3, 15, 8) + dfs(2, 15, 8)

// dfs(->3, 15, 8)
Step 5: if root == NULL
          root -> 3
          false

          currentSum = previousSum + root->val
                     = 15 + 3
                     = 18

          count = 0

          currentSum == targetSum
          18 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->3, 18, 8) + dfs(->(-2), 18, 8)

// dfs(->3, 18, 8)
Step 6: if root == NULL
          root -> 3
          false

          currentSum = previousSum + root->val
                     = 18 + 3
                     = 21

          count = 0

          currentSum == targetSum
          21 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->nil, 21, 8) + dfs(->nil, 21, 8)

         Both dfs(->nil, 21, 8), dfs(->nil, 21, 8) node is nil so we return 0 and backtrack to Step 5
         0 + dfs(->3, 18, 8) + dfs(->(-2), 18, 8) where we solve for
         dfs(->(-2), 18, 8)

// dfs(->(-2), 18, 8)
Step 7: if root == NULL
          root -> -2
          false

          currentSum = previousSum + root->val
                     = 21 + -2
                     = 19

          count = 0

          currentSum == targetSum
          19 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->nil, 19, 8) + dfs(->nil, 19, 8)

          Both dfs(->nil, 19, 8), dfs(->nil, 19, 8) node is nil so we return 0 and backtrack to Step 4
          0 + dfs(->3, 15, 8) + dfs(2, 15, 8) where we solve for
          dfs(2, 15, 8)

// dfs(2, 15, 8)
Step 8: if root == NULL
          root -> 2
          false

          currentSum = previousSum + root->val
                     = 15 + 2
                     = 17

          count = 0

          currentSum == targetSum
          17 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->nil, 17, 8) + dfs(1, 17, 8)

          dfs(->nil, 17, 8) returns 0 as node is nil, so we evaluate for
          dfs(1, 17, 8)

// dfs(1, 17, 8)
Step 9: if root == NULL
          root -> 1
          false

          currentSum = previousSum + root->val
                     = 17 + 1
                     = 18

          count = 0

          currentSum == targetSum
          18 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->nil, 18, 8) + dfs(->nil, 18, 8)

          Both dfs(->nil, 19, 8), dfs(->nil, 19, 8) node is nil so we return 0 and backtrack to Step 3
          0 + dfs(->5, 10, 8) + dfs(->(-3), 10, 8) where we solve for
          dfs(->(-3), 10, 8)

// dfs(->(-3), 10, 8)
Step 10: if root == NULL
          root -> -3
          false

          currentSum = previousSum + root->val
                     = 10 + -3
                     = 7

          count = 0

          currentSum == targetSum
          7 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->nil, 7, 8) + dfs(->11, 7, 8)

          dfs(->nil, 7, 8) returns 0 as node is nil, so we evaluate for
          dfs(->11, 7, 8)

// dfs(->11, 7, 8)
Step 11: if root == NULL
          root -> 11
          false

          currentSum = previousSum + root->val
                     = 7 + 11
                     = 18

          count = 0

          currentSum == targetSum
          18 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->nil, 18, 8) + dfs(->nil, 18, 8)

          Both dfs(->nil, 18, 8), dfs(->nil, 18, 8) node is nil so we return 0 and backtrack to Step 2
          dfs(->10, 0, 8) + pathSum(->5, 8) + pathSum(-3, 8)
          where we have dfs(->10, 0, 8) as 0
          and we evaluate for pathSum(->5, 8)

// pathSum(->5, 8)
Step 12: if root == NULL
          root -> 5
          false

          dfs(root, 0, targetSum) + pathSum(root->left, targetSum) + pathSum(root->right, targetSum)
          dfs(->5, 0, 8) + pathSum(->3, 8) + pathSum(->2, 8)

// dfs(->5, 0, 8)
Step 13: if root == NULL
          root -> 5
          false

          currentSum = previousSum + root->val
                     = 0 + 5
                     = 5

          count = 0

          currentSum == targetSum
          5 == 8
          false

          count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
          0 + dfs(->3, 5, 8) + dfs(->2, 5, 8)

// dfs(->3, 5, 8)
Step 14: if root == NULL
           root -> 3
           false

           currentSum = previousSum + root->val
                      = 5 + 3
                      = 8

           count = 0

           currentSum == targetSum
           8 == 8
           true
           count = 1

           count + dfs(root->left, currentSum, targetSum) + dfs(root->right, currentSum, targetSum)
           1 + dfs(->3, 8, 8) + dfs(->(-2), 8, 8)

We similarly iterate over the rest of the tree and return the count.