LeetCode - Symmetric tree

Problem statement

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

Problem statement taken from: https://leetcode.com/problems/symmetric-tree

Example 1:

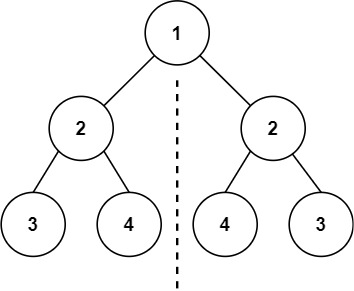
Input: root = [1, 2, 2, 3, 4, 4, 3]
Output: true

Example 2:

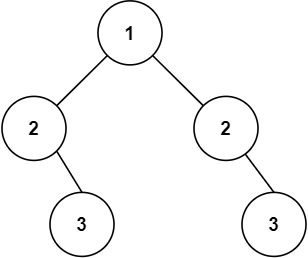
Input: root = [1, 2, 2, null, 3, null, 3]
Output: false

Constraints

- The number of nodes in the tree is in the range [1, 1000].
- -100 <= Node.val <= 100

Explanation

Recursive function

When it comes to solving problems related to trees, recursion is the best choice. If not recursion, the iterative approach will use queues.

Let's explore a simple recursive approach in this blog. The approach is to use two pointers as arguments that points to the root of the tree. The first pointer will move left and second will move right and verify if the nodes are same or not.

Let's check the algorithm.

// main function
- call recursive function areSymmetric(root, root)

// areSymmetric function(root1, root2)
- if !root1 && !root2
  - return true
- else
  - if root1 && root2
    - if root1->val == root2->val
      - return areSymmetric(root1->left, root2->right) && areSymmetric(root1->right, root2->left)

- return false

C++ solution

bool areSymmetric(TreeNode* root1, TreeNode* root2){
    if(!root1 && !root2){
        return true;
    } else {
        if(root1 && root2){
            if(root1->val == root2->val){
                return areSymmetric(root1->left, root2->right) &&
                    areSymmetric(root1->right, root2->left);
            }
        }
        return false;
    }
}

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return areSymmetric(root, root);
    }
};

Golang solution

func areSymmetric(root1 *TreeNode, root2 *TreeNode) bool {
    if root1 == nil && root2 == nil {
        return true
    } else {
        if root1 != nil && root2 != nil {
            if root1.Val == root2.Val {
                return areSymmetric(root1.Left, root2.Right) && areSymmetric(root1.Right, root2.Left)
            }
        }
    }

    return false
}

func isSymmetric(root *TreeNode) bool {
    return areSymmetric(root, root)
}

Javascript solution

var areSymmetric = function(root1, root2) {
    if(!root1 && !root2) {
        return true;
    } else {
        if(root1 && root2) {
            if(root1.val == root2.val) {
               return areSymmetric(root1.left, root2.right) && areSymmetric(root1.right, root2.left);
            }
        }
    }

    return false;
}

var isSymmetric = function(root) {
    return areSymmetric(root, root);
};

Dry Run

Let's dry-run our algorithm to see how the solution works.

Input: root = [1, 2, 2, 3, 4, 4, 3]

// in main function
Step 1: return areSymmetric(root, root)

// in areSymmetric function
Step 2: if !root1 && !root2
          - root1 != nil
            1 != nil
            true

          - root2 != nil
            1 != nil
            true

          - !true && !true
          - false

        else
          if root1 && root2
            - 1 && 1
            - true

            if root1->val == root2->val
               - 1 == 1
               - true

               return areSymmetric(root1->left, root2->right) && areSymmetric(root1->right && root2->left)
               return areSymmetric(2, 2) && areSymmetric(2, 2)

               // we will ignore the 2nd condition here, since both are same.
               // In actual recursive call it will be evaluated.

Step 3: if !root1 && !root2
          - root1 != nil
            2 != nil
            true

          - root2 != nil
            2 != nil
            true

          - !true && !true
          - false

        else
          if root1 && root2
            - 2 && 2
            - true

            if root1->val == root2->val
               - 2 == 2
               - true

            return areSymmetric(root1->left, root2->right) && areSymmetric(root1->right && root2->left)
            return areSymmetric(3, 3) && areSymmetric(4, 4)

// areSymmetric(3, 3)
Step 4: if !root1 && !root2
          - root1 != nil
            3 != nil
            true

          - root2 != nil
            3 != nil
            true

          - !true && !true
          - false

        else
          if root1 && root2
            - 3 && 3
            - true

            if root1->val == root2->val
               - 3 == 3
               - true

            return areSymmetric(root1->left, root2->right) && areSymmetric(root1->right && root2->left)
            return areSymmetric(nil, nil) && areSymmetric(nil, nil)

// areSymmetric(nil, nil)
Step 5: if !root1 && !root2
          - root1 != nil
            nil != nil
            false

          - root2 != nil
            nil != nil
            false

          - !false && !false
          - true

// areSymmetric(4, 4)
Step 6: if !root1 && !root2
          - root1 != nil
            4 != nil
            true

          - root2 != nil
            4 != nil
            true

          - !true && !true
          - false

        else
          if root1 && root2
            - 4 && 4
            - true

            if root1->val == root2->val
               - 4 == 4
               - true

            return areSymmetric(root1->left, root2->right) && areSymmetric(root1->right && root2->left)
            return areSymmetric(nil, nil) && areSymmetric(nil, nil)

            // areSymmetric(nil, nil) returns true
            // so we move back from step 6 to step 5 till step 2 and evaluate

            return areSymmetric(root1->left, root2->right) && areSymmetric(root1->right && root2->left)

            // which is true

So the answer we return is true.