LeetCode - Spiral Matrix
Problem statement
Given an m x n matrix, return all elements of the matrix in spiral order.
Problem statement taken from: https://leetcode.com/problems/spiral-matrix
Example 1:
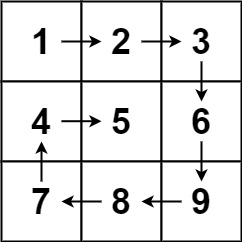
Input: matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
Output: [1, 2, 3, 6, 9, 8, 7, 4, 5]
Example 2:
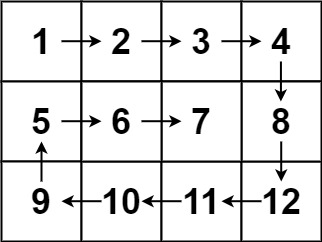
Input: matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
Output: [1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7]
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 10
- -100 <= matrix[i][j] <= 100
Explanation
Clockwise(Spiral) matrix traversal
As per the above examples, we can see the elements of the outer loop are printed first in a clockwise manner then the elements of the inner loop are printed. So the problem can be solved by dividing the matrix into boundaries. We need to use four loops that print the array element in the spiral clockwise form.
Let's check the algorithm:
- set k = 0, l = 0
set m = matrix.size(), n = matrix[0].size()
initialize result array and i
/*
k - starting row index
m - ending row index
l - starting column index
n - ending column index
i - iterator
*/
- loop while k < m && l < n
- loop for i = l; i < n; i++
- result.push(matrix[k][i])
- k++
- loop for i = k; i < m; i++
- result.push(matrix[i][n - 1])
- n--
- if k < m
- loop for i = n - 1; i >= l; i--
- result.push(matrix[m - 1][i])
- m--
- if l < n
- loop for i = m - 1; i >= k; i--
- result.push(matrix[i][l])
- l++
- return result
C++ solution
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int k = 0, l = 0;
int i;
int m = matrix.size();
int n = matrix[0].size();
vector<int> result;
while(k < m && l < n) {
for(i = l; i < n; i++) {
result.push_back(matrix[k][i]);
}
k++;
for(i = k; i < m; i++) {
result.push_back(matrix[i][n - 1]);
}
n--;
if(k < m) {
for(i = n - 1; i >= l; i--) {
result.push_back(matrix[m - 1][i]);
}
m--;
}
if(l < n) {
for(i = m - 1; i >= k; i--) {
result.push_back(matrix[i][l]);
}
l++;
}
}
return result;
}
};
Golang solution
func spiralOrder(matrix [][]int) []int {
m := len(matrix)
n := len(matrix[0])
result := make([]int, m * n)
counter := 0
k , l := 0, 0
var i int
for k < m && l < n {
for i = l; i < n; i++ {
result[counter] = matrix[k][i]
counter++
}
k++
for i = k; i < m; i++ {
result[counter] = matrix[i][n - 1]
counter++
}
n--
if k < m {
for i = n - 1; i >= l; i-- {
result[counter] = matrix[m - 1][i]
counter++
}
m--
}
if l < n {
for i = m - 1; i >= k; i-- {
result[counter] = matrix[i][l]
counter++
}
l++
}
}
return result
}Javascript solution
var spiralOrder = function(matrix) {
let m = matrix.length, n = matrix[0].length;
let result = [];
let k = 0, l = 0, i;
while(k < m && l < n) {
for(i = l; i < n; i++) {
result.push(matrix[k][i]);
}
k++;
for(i = k; i < m; i++) {
result.push(matrix[i][n - 1]);
}
n--;
if(k < m) {
for(i = n - 1; i >= l; i--) {
result.push(matrix[m - 1][i]);
}
m--;
}
if(l < n) {
for(i = m - 1; i >= k; i--) {
result.push(matrix[i][l]);
}
l++;
}
}
return result;
};
Dry Run
Let's dry-run our algorithm to see how the solution works.
Input: matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
Step 1: k = 0, l = 0, i
m = matrix.size()
= 3
n = matrix[0].size()
= 3
initialize vector<int> result
Step 2: loop while k < m && l < n
0 < 3 && 0 < 3
true
loop for i = l; i < n; i++
result.push_back(matrix[k][i])
// the for loop iterates for i = 0 to 2
// we fetch matrix[0][0], matrix[0][1] and matrix[0][2]
result = [1, 2, 3]
k++
k = 1
loop for i = k; i < m; i++
result.push_back(matrix[i][n - 1])
// the for loop iterates for i = 1 to 2
// we fetch matrix[1][2] and matrix[2][2]
result = [1, 2, 3, 6, 9]
n--
n = 2
if k < m
1 < 3
true
loop for i = n - 1; i >= l; i--
result.push_back(matrix[m - 1][i])
// the for loop iterates for i = 2 to 0
// we fetch matrix[2][1] and matrix[2][0]
result = [1, 2, 3, 6, 9, 8, 7]
m--
m = 2
if l < n
0 < 2
true
loop for i = m - 1; i >= k; i--
result.push_back(matrix[i][l])
// the for loop iterates for i = 1 to 1
// we fetch matrix[1][0]
result = [1, 2, 3, 6, 9, 8, 7, 4]
l++
l = 1
Step 3: loop while k < m && l < n
1 < 2 && 1 < 2
true
loop for i = l; i < n; i++
result.push_back(matrix[k][i])
// the for loop iterates for i = 1 to 1
// we fetch matrix[1][1]
result = [1, 2, 3, 6, 9, 8, 7, 4, 5]
k++
k = 2
loop for i = k; i < m; i++
result.push_back(matrix[i][n - 1])
// no iteration as k is 2 and m is 2
// i = k; i = 2 and 2 < 2 false
n--
n = 1
if k < m
2 < 3
true
loop for i = n - 1; i >= l; i--
result.push_back(matrix[m - 1][i])
// no iteration as n is 1 and l is 1
// i = n - 1; i = 0 and 0 >= 1 false
m--
m = 1
if l < n
1 < 1
false
l++
l = 2
Step 4: loop while k < m && l < n
2 < 1 && 2 < 1
false
Step 5: return result
So we return the answer as [1, 2, 3, 6, 9, 8, 7, 4, 5].