Odd Even Linked List

Problem statement

Given the head of a singly linked list, group all the nodes with odd indices together followed by the nodes with even indices, and return the reordered list.

The first node is considered odd, and the second node is even, and so on.

Note that the relative order inside both the even and odd groups should remain as it was in the input.

You must solve the problem in O(1) extra space complexity and O(n) time complexity.

Problem statement taken from: https://leetcode.com/problems/odd-even-linked-list.

Example 1:

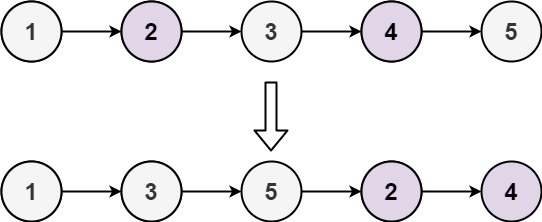
Input: head = [1, 2, 3, 4, 5]
Output: [1, 3, 5, 2, 4]

Example 2:

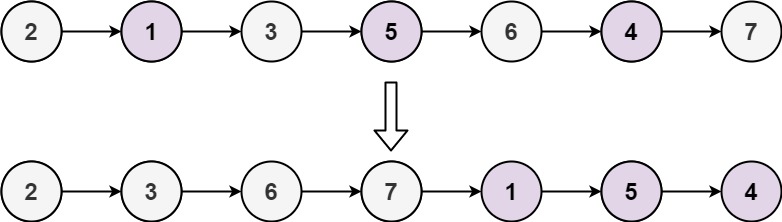
Input: head = [2, 1, 3, 5, 6, 4, 7]
Output: [2, 3, 6, 7, 1, 5, 4]

Constraints:

- The number of nodes in the linked list is in the range [0, 10^4].
- -10^6 <= Node.val <= 10^6

Solution

Approach 1: Using additional

The naive approach is to create two separate linked lists, one for the odd-indices nodes and the other for the even-indices nodes. We iterate the original linked list, and for each node, we will check the node's position using a counter. If the linked list position node is odd, we append it to the odd-indices linked list, or if the position is even, we append it to the even-indices linked list. Once the complete linked list is traversed, we append the even-indices linked list at the end of the odd-indices linked list.

A C++ snippet of this approach is as follows:

ListNode* oddEvenList(ListNode* head) {
    // initialize oddHead and evenHead pointers
    ListNode* oddHead = new ListNode(0);
    ListNode* odd = oddHead;
    ListNode* evenHead = new ListNode(0);
    ListNode* even = evenHead;
    ListNode* currend = head;
    int counter = 1;

    // traverse the linked list till the end
    while(current) {
        // odd-indices node
        if(counter % 2 == 1) {
            odd->next = current;
            odd = odd->next;
        } else {
            // even-indices node
            even->next = current;
            even = even->next;
        }

        current = current->next;
        counter++;
    }

    // append even-indices linked list
    // at the end of the odd-indices linked list
    odd->next = evenHead->next;
    even->next = NULL;

    return oddHead->next;
};

The time complexity of the above algorithm is O(n), and the space complexity is O(1).

Approach 2: Sorting in-place

We can tweak the above algorithm to solve the odd-even linked list problem. The counter variable can be eliminated, and instead of pointing the oddHead and evenHead to a new node, we can point them to head and head->next, respectively.

When working on the solution, it’s important to ensure we are covering all the edge cases.

1. Empty linked list or a linked list with a single node.
2. A linked list with only two nodes.
3. A linked list with odd numbers of nodes.
4. A linked list with an even number of nodes.

Let's check the algorithm first.

Algorithm

// if the list is empty or has only one node
- if head == NULL || head->next == NULL
  - return head
- end if

// initialize the odd and even pointers
- oddPointer = head
  evenPointer = head->next
  evenHead = head->next

// loop while even pointer is not NULL
// or even pointer next is not NULL
- loop while evenPointer != NULL && evenPointer->next != NULL

  // skip the next node and point the current odd index node to
  // the next odd index node
  - oddPointer->next = oddPointer->next->next
  - oddPointer = oddPointer->next

  // skip the next node and point the current even index node to
  // the even odd index node
  - evenPointer->next = evenPointer->next->next
  - evenPointer = evenPointer->next
- while end

- oddPointer->next = evenHead

- return head

We initialized three-pointers oddPointer, evenPointer and evenHead. oddPointer will point to the head and the evenPointer will point to the head's next node. In each iteration, the oddPointer and evenPointer will skip the next node point to the next odd and even index node. Once the iteration over the linked list is done, we point the oddPointer next to the start of evenHead.

The time complexity of the above algorithm is O(n), and the space complexity is O(1).

Let's check out our solutions in C++, Golang, and Javascript.

C++ solution

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* oddEvenList(ListNode* head) {
        // if the list is empty or has only one node
        if(head == NULL || head->next == NULL) {
            return head;
        }

        // initialize the odd and even pointers
        ListNode* oddPointer = head;
        ListNode* evenPointer = head->next;
        ListNode* evenHead = head->next;

        // loop while even pointer is not NULL
        // or even pointer next is not NULL
        while(evenPointer != NULL && evenPointer->next != NULL) {

            // skip the next node and point the current odd index node to
            // the next odd index node
            oddPointer->next = oddPointer->next->next;
            oddPointer = oddPointer->next;

            // skip the next node and point the current even index node to
            // the even odd index node
            evenPointer->next = evenPointer->next->next;
            evenPointer = evenPointer->next;
        }

        oddPointer->next = evenHead;

        return head;
    }
};

Go solution

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func oddEvenList(head *ListNode) *ListNode {
    // if the list is empty or has only one node
    if head == nil || head.Next == nil {
        return head
    }

    // initialize the odd and even pointers
    oddPointer, evenPointer, evenHead := head, head.Next, head.Next

    // loop while even pointer is not NULL
    // or even pointer next is not NULL
    for evenPointer != nil && evenPointer.Next != nil {
        // skip the next node and point the current odd index node to
        // the next odd index node
        oddPointer.Next = oddPointer.Next.Next
        oddPointer = oddPointer.Next

        // skip the next node and point the current even index node to
        // the even odd index node
        evenPointer.Next = evenPointer.Next.Next
        evenPointer = evenPointer.Next
    }

    oddPointer.Next = evenHead

    return head
}

JavaScript solution

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var oddEvenList = function(head) {
    // if the list is empty or has only one node
    if(head == null || head.next == null) {
        return head;
    }

    // initialize the odd and even pointers
    let oddPointer = head;
    let evenPointer = head.next;
    let evenHead = head.next;

    // loop while even pointer is not NULL
    // or even pointer next is not NULL
    while(evenPointer != null && evenPointer.next != null) {
        // skip the next node and point the current odd index node to
        // the next odd index node
        oddPointer.next = oddPointer.next.next;
        oddPointer = oddPointer.next;

        // skip the next node and point the current even index node to
        // the even odd index node
        evenPointer.next = evenPointer.next.next;
        evenPointer = evenPointer.next;
    }

    oddPointer.next = evenHead;

    return head;
};

Dry Run

Let's dry-run our algorithm to see how the solution works.

Input: head = [1, 2, 3, 4, 5]

Step 1: if head == NULL || head->next == NULL
           head -> 1
           head->next -> 2
           false

Step 2: ListNode* oddPointer = head
                  oddPointer -> 1

        ListNode* evenPointer = head->next
                  evenPointer -> 2

        ListNode* evenHead = head->next
                  evenHead -> 2

Step 3: loop while evenPointer != NULL && evenPointer->next != NULL
          evenPointer -> 2
          evenPointer->next -> 4

          2 != NULL && 4 != NULL
          true

          oddPointer->next = oddPointer->next->next
          oddPointer->next -> 2
          oddPointer->next->next -> 3

          oddPointer -> 1 -> 3

          oddPointer = oddPointer->next
          oddPointer -> 3

          evenPointer->next = evenPointer->next->next
          evenPointer->next -> 3
          evenPointer->next->next -> 4

          evenPointer -> 2 -> 4

          evenPointer = evenPointer->next
          evenPointer -> 4

Step 4: loop while evenPointer != NULL && evenPointer->next != NULL
          evenPointer -> 4
          evenPointer->next -> 5

          2 != NULL && 5 != NULL
          true

          oddPointer->next = oddPointer->next->next
          oddPointer->next -> 4
          oddPointer->next->next -> 5

          oddPointer -> 1 -> 3 -> 5

          oddPointer = oddPointer->next
          oddPointer -> 5

          evenPointer->next = evenPointer->next->next
          evenPointer->next -> 5
          evenPointer->next->next -> NULL

          evenPointer -> 2 -> 4 -> NULL

          evenPointer = evenPointer->next
          evenPointer -> NULL

Step 5: loop while evenPointer != NULL && evenPointer->next != NULL
          evenPointer -> NULL

          NULL != NULL
          false

Step 6: oddPointer->next = evenHead
        1 -> 3 -> 5 -> 2 -> 4

Step 7: return head

We return the answer as 1 -> 3 -> 5 -> 2 -> 4.