LeetCode - Lowest Common Ancestor of a Binary Search Tree

Problem statement

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).

Problem statement taken from: https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/

Example 1:

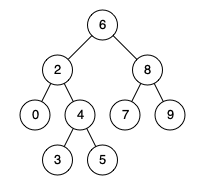
Input: root = [6, 2, 8, 0, 4, 7, 9, null, null, 3, 5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

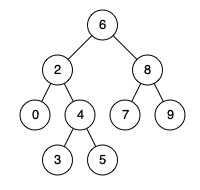
Input: root = [6, 2, 8, 0, 4, 7, 9, null, null, 3, 5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2, 1], p = 2, q = 1
Output: 2

Constraints:

- The number of nodes in the tree is in the range [2, 10^5]
- -10^9 <= Node.val <= 10^9
- All Node.val are unique
- p != q
- p and q will exist in the BST

Explanation

Storing paths

The solution in this approach is to store the path from the root to p and root to q in two separate arrays. We then find the first element in the arrays that are mismatched.

For Example 2:

The path from the root to 2: [6, 2]

The path from the root to 4: [6, 2, 4]

We find the first element: 6 matches. We check the next element, which is 2, and it matches. The array for path root to 2 is done, and the array for path root to 4 has an element at the 2nd index; we consider it a mismatch.

We return the last element in both the arrays that match, which is 2.

A C++ snippet of the above approach is as follows:

bool findPath(Node* root, vector<int>& path, int k) {
    if (root == NULL) {
        return false;
    }

    path.push_back(root->val);

    if (root->val == k) {
        return true;
    }

    if ((root->left && findPath(root->left, path, k))
        || (root->right && findPath(root->right, path, k))) {
        return true;
    }

    path.pop_back();
    return false;
}

int findLCA(Node* root, int p, int q) {
    vector<int> path1, path2;
    int i;

    if (!findPath(root, path1, p)
        || !findPath(root, path2, q)) {
        return -1;
    }

    for (i = 0; i < path1.size() && i < path2.size(); i++)
        if (path1[i] != path2[i])
            break;

    return path1[i - 1];
}

The time complexity and the space complexity of the above approach is O(n).

Single Traversal

We use preorder traversal and solve the problem using below steps:

• We check if the value of the root matches p and q
  • If yes, we return the root
  • else we recursively call the left and right subtree
• If there is any root that returns one NULL and one NON-NULL value, we return the corresponding NON-NULL value for that node.
• The root that returns both NON-NULL values for both the left and right subtree, is our LCA.

A C++ snippet of the above approach is as follows:

struct Node* findLCA(struct Node* root, int p, int q) {
    if (root == NULL)
        return NULL;

    if (root->key == p || root->key == q)
        return root;

    Node* leftLCA = findLCA(root->left, p, q);
    Node* rightLCA = findLCA(root->right, p, q);

    if (leftLCA && rightLCA) {
        return root;
    }

    return (leftLCA != NULL) ? leftLCA : rightLCA;
}

The time complexity of the above approach is O(n), and the space complexity is O(h), where h is the tree's height.

Recursion

The problem statement states that the tree is a Binary Search Tree (BST). We can modify the above recursive approach to avoid unnecessary calls to the left and right subtree.

Let's check the algorithm first.

- if root == null
  - return null

- if root->val > p->val && root->val > q->val
  - return lca(root->left, p, q)

- if root->val < p->val && root->val < q->val
  - return lca(root->right, p, q)

- return root

This approach's time and space complexity are O(h), where h is the tree's height.

Let's check our algorithm in C++, Golang, and JavaScript.

C++ solution

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL) {
            return NULL;
        }

        if(root->val > p->val && root->val > q->val) {
            return lowestCommonAncestor(root->left, p, q);
        }

        if(root->val < p->val && root->val < q->val) {
            return lowestCommonAncestor(root->right, p, q);
        }

        return root;
    }
};

Golang solution

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
	if root == nil {
        return nil
    }

    if root.Val > p.Val && root.Val > q.Val {
        return lowestCommonAncestor(root.Left, p, q)
    }

    if root.Val < p.Val && root.Val < q.Val {
        return lowestCommonAncestor(root.Right, p, q)
    }

    return root
}

JavaScript solution

var lowestCommonAncestor = function(root, p, q) {
    if(root === null) {
        return null;
    }

    if(root.val > p.val && root.val > q.val) {
        return lowestCommonAncestor(root.left, p, q);
    }

    if(root.val < p.val && root.val < q.val) {
        return lowestCommonAncestor(root.right, p, q);
    }

    return root;
};

Dry Run

Let's dry-run our algorithm to see how the solution works.

Input: root = [6, 2, 8, 0, 4, 7, 9, null, null, 3, 5]
       p = 2
       q = 4

Step 1: if root == NULL
          root -> 6
          false

        if root->val > p->val && root->val > q->val
          6 > 2 && 6 > 4
          true

          return lowestCommonAncestor(root->left, p, q)
               lowestCommonAncestor(->2, ->2, ->4)

// lowestCommonAncestor(->2, ->2, ->4)
Step 2: if root == NULL
          root -> 2
          false

        if root->val > p->val && root->val > q->val
          2 > 2 && 2 > 4
          false

        if root->val < p->val && root->val < q->val
          2 < 2 && 2 < 4
          false

        return root

        We backtrack to Step 1

Step 3: return lowestCommonAncestor(root->left, p, q)
               lowestCommonAncestor(->2, ->2, ->4)
               2

We return the answer as 2.