LeetCode - Construct Binary Tree from Preorder and Inorder Traversal
Problem statement
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
Problem statement taken from: https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal
Example 1:
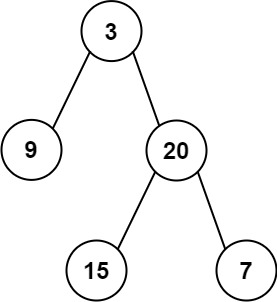
Input: preorder = [3, 9, 20, 15, 7], inorder = [9, 3, 15, 20, 7]
Output: [3, 9, 20, null, null, 15, 7]
Example 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
Constraints:
- 1 <= preorder.length <= 3000
- inorder.length == preorder.length
- -3000 <= preorder[i], inorder[i] <= 3000
- preorder and inorder consist of unique values.
- Each value of inorder also appears in preorder.
- preorder is guaranteed to be the preorder traversal of the tree.
- inorder is guaranteed to be the inorder traversal of the tree.
Explanation
Brute force approach
The preorder sequence pattern is root-left-right and the inorder sequence is left-root-right. Node 3 in this preorder sequence [3, 9, 20, 15, 7] is the root. We search for node 3 in the inorder sequence. All the elements to the left of 3 in the inorder sequence belong to the left subtree and the elements to the right of it belong to the right subtree.
A C++ snippet of this approach is as follows:
TreeNode* buildTree(int inorder[], int preorder[], int inStart, int inEnd) {
static int preIndex = 0;
if (inStart > inEnd)
return NULL;
TreeNode* node = newNode(preorder[preIndex++]);
if (inStart == inEnd)
return node;
int inIndex = search(inorder, inStart, inEnd, node->data);
node->left = buildTree(inorder, preorder, inStart, inIndex - 1);
node->right = buildTree(inorder, preorder, inIndex + 1, inEnd);
return node;
}
int search(int arr[], int start, int end, char value) {
int i;
for (i = start; i <= end; i++) {
if (arr[i] == value)
return i;
}
}The time complexity of this approach is O(n^2). The space complexity is O(n). The extra space is due to the recursive call stack.
Efficient solution: Using Map
We can optimize the search function by using hashing. We store the indexes of inorder sequence in a hash map.
A C++ snippet of this approach is as follows:
TreeNode* buildTree(int inorder[], int preorder[], int inStart, int inEnd, unordered_map<int, int>& mp) {
int preIndex = 0;
if (inStart > inEnd)
return NULL;
int current = preorder[preIndex++];
TreeNode* tNode = newNode(current);
if (inStart == inEnd)
return tNode;
int inIndex = mp[current];
tNode->left = buildTree(inorder, preorder, inStart, inIndex - 1, mp);
tNode->right = buildTree(inorder, preorder, inIndex + 1, inEnd, mp);
return tNode;
}The time complexity of this approach is O(n). The space complexity is O(n). The extra space is used to store the elements in the map also due to the recursive function call stack.
Efficient solution: Using Stack
Instead of a map, we can also solve the problem using a stack and set. The stack will be used to store the path we traversed when iterating over the preorder array, and the set is used to maintain the node in which the next right subtree is expected.
Let's check the algorithm to understand it better.
Algorithm
- set TreeNode* root, node = NULL, NULL
create a set<TreeNode*> s
create a stack TreeNode* st
set n = preorder.size()
- loop for pre = 0, in = 0; pre < n
- set node = NULL
- loop do
- node = new TreeNode(preorder[pre])
- if root == NULL
- root = node
- if end
- if st.size() > 0
- if s.find(st.top()) != s.end()
- s.erase(st.top())
- st.top()->right = node
- st.pop()
- else
- st.top()->left = node
- if end
- if end
- st.push(node)
- while preorder[pre++] != inorder[in] && pre < n
- set node = NULL
- loop while st.size() > 0 && in < n && st.top()->val == inorder[in]
- node = st.top()
- st.pop()
- in++
- while end
- if node != NULL
- s.insert(node)
- st.push(node)
- if end
- for end
- return root
Let's check out our solutions in C++, Golang, and Javascript.
C++ solution
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
TreeNode* root = NULL;
TreeNode* node = NULL;
set<TreeNode*> s;
stack<TreeNode*> st;
int n = preorder.size();
for (int pre = 0, in = 0; pre < n;) {
node = NULL;
do {
node = new TreeNode(preorder[pre]);
if (root == NULL) {
root = node;
}
if (st.size() > 0) {
if (s.find(st.top()) != s.end()) {
s.erase(st.top());
st.top()->right = node;
st.pop();
} else {
st.top()->left = node;
}
}
st.push(node);
} while (preorder[pre++] != inorder[in] && pre < n);
node = NULL;
while(st.size() > 0 && in < n && st.top()->val == inorder[in]) {
node = st.top();
st.pop();
in++;
}
if(node != NULL) {
s.insert(node);
st.push(node);
}
}
return root;
}
};Golang solution
We are using a map instead of a set here.
func buildTree(preorder []int, inorder []int) *TreeNode {
n := len(preorder)
if n == 0 {
return nil
} else if n == 1 {
return &TreeNode{Val: preorder[0]}
}
root := &TreeNode{Val: preorder[0]}
st := []*TreeNode{root}
m := make(map[int]int)
for i := 0; i < n; i++ {
m[inorder[i]] = i
}
var pop *TreeNode
for i := 1; i < n; i++ {
if m[preorder[i]] < m[st[len(st) - 1].Val] {
pop = st[len(st) - 1]
pop.Left = &TreeNode{Val: preorder[i]}
st = append(st, pop.Left)
continue
}
pop = st[len(st) - 1]
st = st[:len(st) - 1]
for len(st) > 0 && m[preorder[i]] > m[st[len(st)-1].Val] {
pop = st[len(st) - 1]
st = st[:len(st) - 1]
}
pop.Right = &TreeNode{Val: preorder[i]}
st = append(st, pop.Right)
}
return root
}JavaScript solution
var buildTree = function(preorder, inorder) {
let set = new Set();
let stack = [];
let root = null;
let node = null;
let n = preorder.length;
for (let pre = 0, inOrder = 0; pre < n;) {
node = null;
do {
node = new TreeNode(preorder[pre]);
if (root == null) {
root = node;
}
if (stack.length != 0) {
if (set.has(stack[stack.length - 1])) {
set.delete(stack[stack.length - 1]);
stack.pop().right = node;
} else {
stack[stack.length - 1].left = node;
}
}
stack.push(node);
} while (preorder[pre++] != inorder[inOrder] && pre < preorder.length);
node = null;
while (stack.length != 0 && inOrder < n && stack[stack.length - 1].val == inorder[inOrder]) {
node = stack.pop();
inOrder++;
}
if (node != null) {
set.add(node);
stack.push(node);
}
}
return root;
};Dry Run
Let's dry-run our algorithm for a few examples to see how the solution works.
Input: preorder = [3, 9, 20, 15, 7]
inorder = [9, 3, 15, 20, 7]
Step 1: TreeNode* root = NULL
TreeNode* node = NULL
set<TreeNode*> s
stack<TreeNode*> st
int n = preorder.size()
n = 5
Step 2: loop for pre = 0, in = 0; pre < n
0 < 5
true
loop do
node = new TreeNode(preorder[pre])
= new TreeNode(preorder[0])
= new TreeNode(3)
if root == NULL
true
root = node
= ->3
if st.size() > 0
0 > 0
false
st.push(node)
st.push(->3)
st = [3]
while preorder[pre++] != inorder[in] && pre < n
preorder[0] != inorder[0] && 1 < 5
3 != 9 && true
true
node = new TreeNode(preorder[pre])
= new TreeNode(preorder[1])
= new TreeNode(9)
if root == NULL
3 == NULL
false
if st.size() > 0
1 > 0
true
if s.find(st.top()) != s.end()
s = []
st.top = 3
s.find(st.top()) != s.end()
s.find(3) != s.end()
false
else
st.top()->left = node
3->left = 9
if end
st.push(node)
st.push(9)
st = [3, 9]
while preorder[pre++] != inorder[in] && pre < n
preorder[1] != inorder[0] && 2 < 5
9 != 9 && true
false
do end
node = NULL
loop while st.size() > 0 && in < n && st.top()->val == inorder[in]
2 > 0 && 0 < 5 && st.top()->val == inorder[in]
true && true && 9 == inorder[0]
true && 9 == 9
true
node = st.top()
= 9
st.pop()
st = [3]
in++
in = 1
while st.size() > 0 && in < n && st.top()->val == inorder[in]
1 > 0 && 1 < 5 && 3 == inorder[1]
true && true && 3 == 3
true
node = st.top()
= 3
st.pop()
st = []
in++
in = 2
while st.size() > 0 && in < n && st.top()->val == inorder[in]
0 > 0 && 2 < 5
false
while end
if node != NULL
3 != NULL
true
s.insert(node)
s.insert(3)
s = [3]
st.push(node)
st.push(3)
st = [3]
Step 3: loop for pre < n
2 < 5
true
node = NULL
loop do
node = new TreeNode(preorder[pre])
= new TreeNode(preorder[2])
= new TreeNode(20)
if root == NULL
3 == NULL
false
if st.size() > 0
1 > 0
true
if s.find(st.top()) != s.end()
s = [3]
st.top() = 3
s.find(3) != s.end()
true
s.erase(st.top())
s.erase(3)
s = []
st.top()->right = node
3->right = 20
st.pop()
st = []
st.push(node)
st = [20]
while preorder[pre++] != inorder[in] && pre < n
preorder[2] != inorder[2] && 3 < 5
20 != 15 && true
true
node = new TreeNode(preorder[pre])
= new TreeNode(preorder[3])
= new TreeNode(15)
if root == NULL
3 == NULL
false
if st.size() > 0
1 > 0
true
if s.find(st.top()) != s.end()
s = []
st.top() = 20
s.find(20) != s.end()
false
else
st.top()->left = node
20->left = 15
st.push(node)
st = [20, 15]
while preorder[pre++] != inorder[in] && pre < n
preorder[3] != inorder[2] && 4 < 5
15 != 15 && true
false
do end
node = NULL
loop while st.size() > 0 && in < n && st.top()->val == inorder[in]
2 > 0 && 2 < 5 && 15 == inorder[2]
true && 15 == 15
node = st.top()
= 15
st.pop()
st = [20]
in++
in = 3
loop while st.size() > 0 && in < n && st.top()->val == inorder[in]
1 > 0 && 3 < 5 && 20 == inorder[3]
true && 20 == 20
true
node = st.top()
= 20
st.pop()
st = []
in++
in = 4
loop while st.size() > 0 && in < n && st.top()->val == inorder[in]
0 > 0
false
if node != NULL
15 != NULL
true
s.insert(node)
s.insert(15)
s = [15]
st.push(node)
st.push(15)
st = [15]
Step 4: loop for pre < n
4 < 5
true
node = NULL
loop do
node = new TreeNode(preorder[pre])
= new TreeNode(preorder[4])
= new TreeNode(7)
if root == NULL
3 == NULL
false
if st.size() > 0
1 > 0
true
if s.find(st.top()) != s.end()
s = [15]
st.top() = 15
s.find(st.top()) != s.end()
true
s.erase(st.top())
s.erase(15)
s = []
st.top()->right = node
15->right = 7
st.pop()
st = []
st.push(node)
st = [7]
while preorder[pre++] != inorder[in] && pre < n
preorder[4] != inorder[4] && 5 < 5
7 != 7 && false
false
node = NULL
loop while st.size() > 0 && in < n && st.top()->val == inorder[in]
1 > 0 && 4 < 5 && 7 == inorder[4]
true && 7 == 7
true
node = st.top()
= 7
st.pop()
st = []
in++
in = 5
loop while st.size() > 0 && in < n && st.top()->val == inorder[in]
0 > 0
false
if node != NULL
7 != NULL
true
s.insert(node)
s = [7]
st.push(node)
st = [7]
Step 5: loop for pre < n
5 < 5
false
Step 6: return root
We return the answer as [3, 9, 20, null, null, 15, 7].