LeetCode - Best Time to Buy and Sell Stock
Problem statement
You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
Problem statement taken from: https://leetcode.com/problems/best-time-to-buy-and-sell-stock
Example 1:
Input: prices = [7, 1, 5, 3, 6, 4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
Example 2:
Input: prices = [7, 6, 4, 3, 1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.
Constraints:
- 1 <= prices.length <= 10^5
- 0 <= prices[i] <= 10^4
Explanation
Brute force approach
The naive approach is to use two nested for loops and get the maximum difference between two numbers.
A C++ snippet of the above approach is as below:
int maxProfit = 0;
for (int i = 0; i < prices.length - 1; i++) {
for (int j = i + 1; j < prices.length; j++) {
int profit = prices[j] - prices[i];
if (profit > maxProfit)
maxProfit = profit;
}
}
return maxProfit;The time complexity of the above program is O(N^2).
One pass approach
If we check the below image of the stock values across days, we need to consider the maximum and minimum values.
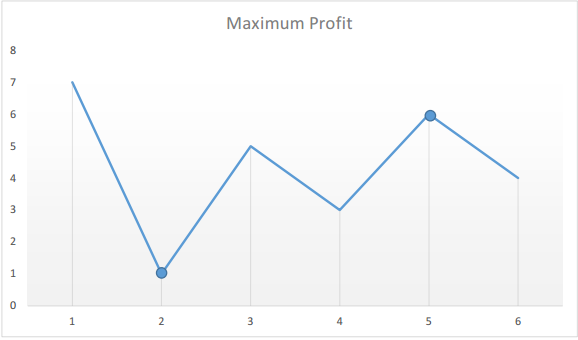
Let's check the algorithm below:
- set maxP = 0
minP = INT_MAX
- loop for i = 0; i < prices.size(); i++
- minP = min(minP, prices[i])
- if prices[i] > minP
- maxP = max(maxP, prices[i] - minP)
- return maxP
The time complexity of the above approach is O(log(N)) and, space complexity is O(1).
C++ solution
class Solution {
public:
int maxProfit(vector<int>& prices) {
int maxP = 0;
int minP = INT_MAX;
for(int i = 0; i < prices.size(); i++){
minP = min(minP, prices[i]);
if(prices[i] > minP){
maxP = max(maxP, prices[i] - minP);
}
}
return maxP;
}
};Golang solution
const MaxUint = ^uint(0)
const MaxInt = int(MaxUint >> 1)
func maxProfit(prices []int) int {
maxP := 0
minP := MaxInt
for i := 0; i < len(prices); i++ {
minP = int(math.Min(float64(minP), float64(prices[i])))
if prices[i] > minP {
maxP = int(math.Max(float64(maxP), float64(prices[i] - minP)))
}
}
return maxP
}Javascript solution
var maxProfit = function(prices) {
let maxP = 0;
let minP = Number.MAX_VALUE;
for( let i = 0; i < prices.length; i++ ) {
minP = Math.min(minP, prices[i]);
if( prices[i] > minP ) {
maxP = Math.max(maxP, prices[i] - minP);
}
}
return maxP;
};Dry Run
Let's dry-run our algorithm to see how the solution works.
Input: prices = [7, 1, 5, 3, 6, 4]
Step 1: maxP = 0
minP = INT_MAX
Step 2: loop for i = 0; i < prices.size()
0 < 6
true
minP = min(minP, prices[i]);
= min(INT_MAX, prices[0])
= min(INT_MAX, 7)
= 7
if prices[i] > minP
prices[0] > 7
7 > 7
false
i++
i = 1
Step 3: loop for i < prices.size()
1 < 6
true
minP = min(minP, prices[i]);
= min(7, prices[1])
= min(7, 1)
= 1
if prices[i] > minP
prices[1] > 1
1 > 1
false
i++
i = 2
Step 4: loop for i < prices.size()
2 < 6
true
minP = min(minP, prices[i]);
= min(1, prices[2])
= min(1, 5)
= 1
if prices[i] > minP
prices[2] > 1
5 > 1
true
maxP = max(maxP, prices[i] - minP)
= max(0, 5 - 1)
= max(0, 4)
= 4
i++
i = 3
Step 5: loop for i < prices.size()
3 < 6
true
minP = min(minP, prices[i]);
= min(1, prices[3])
= min(1, 3)
= 1
if prices[i] > minP
prices[3] > 1
3 > 1
true
maxP = max(maxP, prices[i] - minP)
= max(4, 3 - 1)
= max(4, 2)
= 4
i++
i = 4
Step 6: loop for i < prices.size()
4 < 6
true
minP = min(minP, prices[i]);
= min(1, prices[4])
= min(1, 6)
= 1
if prices[i] > minP
prices[4] > 1
6 > 1
true
maxP = max(maxP, prices[i] - minP)
= max(4, 6 - 1)
= max(4, 5)
= 5
i++
i = 5
Step 7: loop for i < prices.size()
5 < 6
true
minP = min(minP, prices[i]);
= min(1, prices[5])
= min(1, 4)
= 1
if prices[i] > minP
prices[5] > 1
4 > 1
true
maxP = max(maxP, prices[i] - minP)
= max(5, 4 - 1)
= max(5, 3)
= 5
i++
i = 6
Step 8: loop for i < prices.size()
6 < 6
false
Step 9: return maxP
So we return the answer as 5.